01 故事起源

一只小猴子边上有100根香蕉，此地距离它家50米，小猴想搬香蕉回家，但有以下几个条件：

• 每次最多搬运50根香蕉
• 每走1m就要吃掉一根香蕉

请问小猴子最多能把多少根香蕉搬回家？

02 初步思考

小猴子最多只能搬50根香蕉，那就搬起50根香蕉往家走。

可以发现，剩余香蕉和行走距离之间是线性关系。最终走到家，剩余香蕉数目为0根。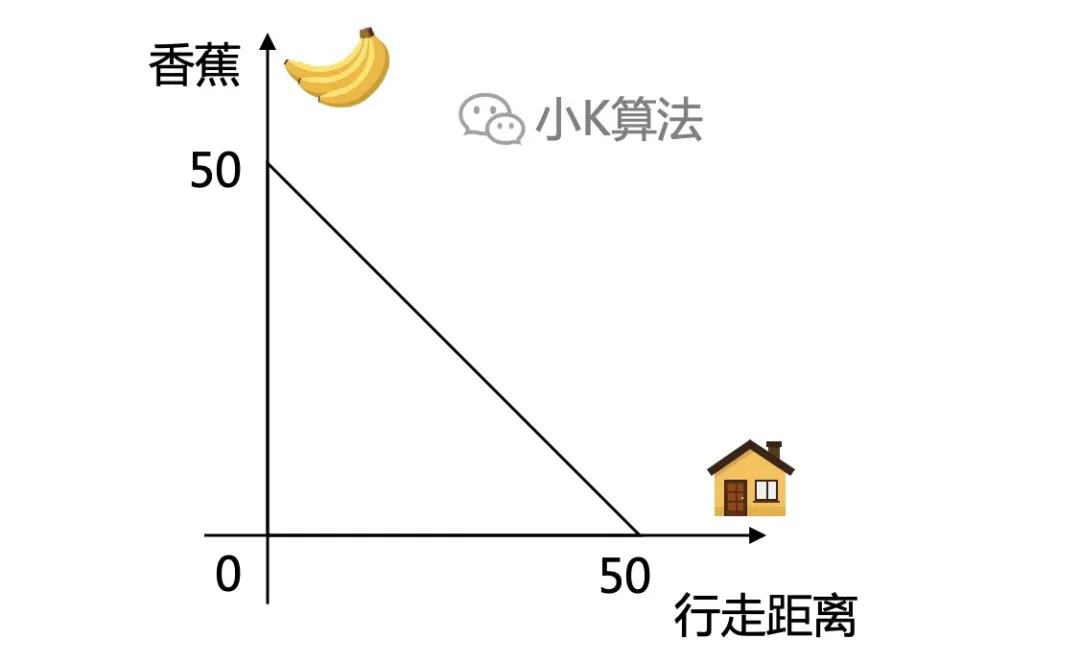

小猴子搬运香蕉的过程可以看成是运输过程，之所以出现上面的问题，就在于运输效率会线性下降，快到家时，虽然身上只有几根香蕉，但油耗（吃掉香蕉数目）依然不变。
因此解决的办法是通过中转来提高运输效率，尽量载满。

03 建立中转站

总共100根，所以转运最多2趟。而且小猴同学不用返回出发地，所以中转地与出发地之间往返3次。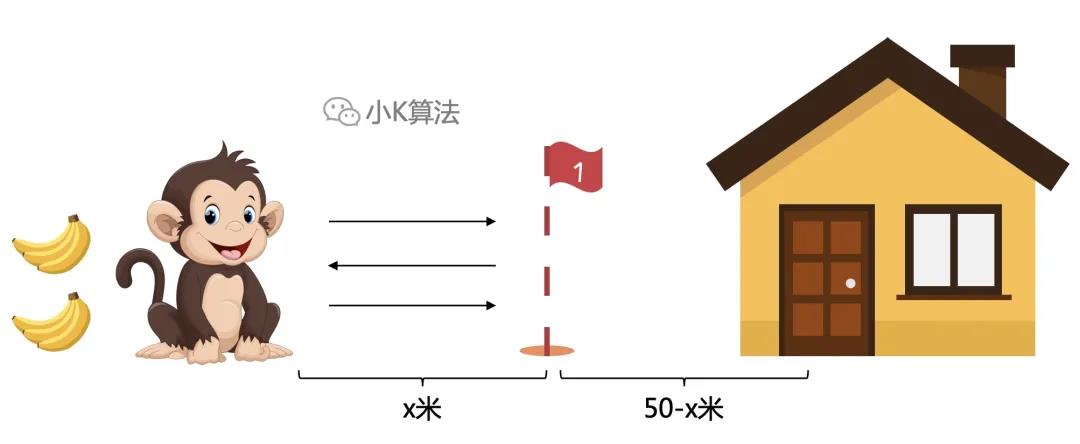

中转是为了下一次能够一次运输完，所以到达中转地之后，香蕉数要小于等于50。
设到中转站距离开始位置x米，则100-3x<=50，x=17米。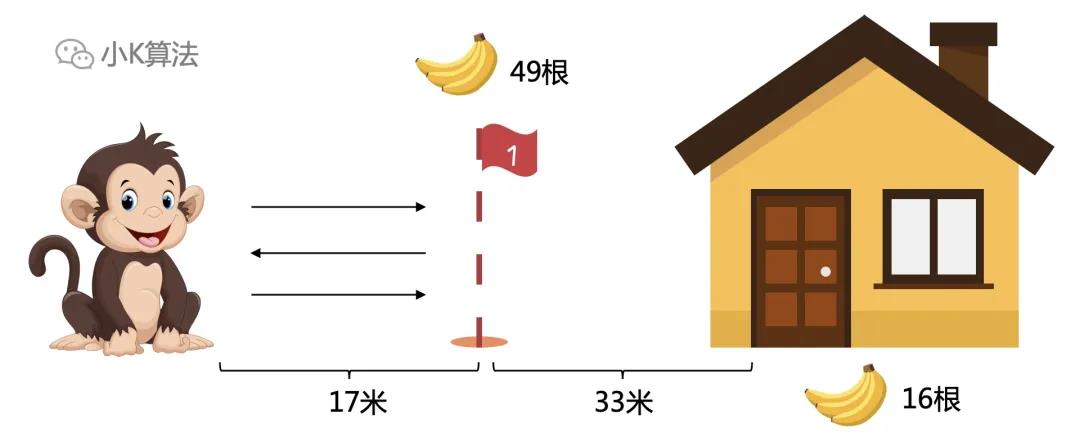

所以第一次搬50到17米处吃掉17根香蕉，再拿17根香蕉返回出发地，此时中转站留下16根香蕉。第二次搬50根到中转站剩下33根，总共49根。然后拿上49根回家，还剩下16根。

04 深入思考

这里借用一下微分的思想，将中转无限分段，假设每隔1米转运1次，那么每一段之间都是往返3次。如果再把这些区间积起来，其实就和上面的思想一样了。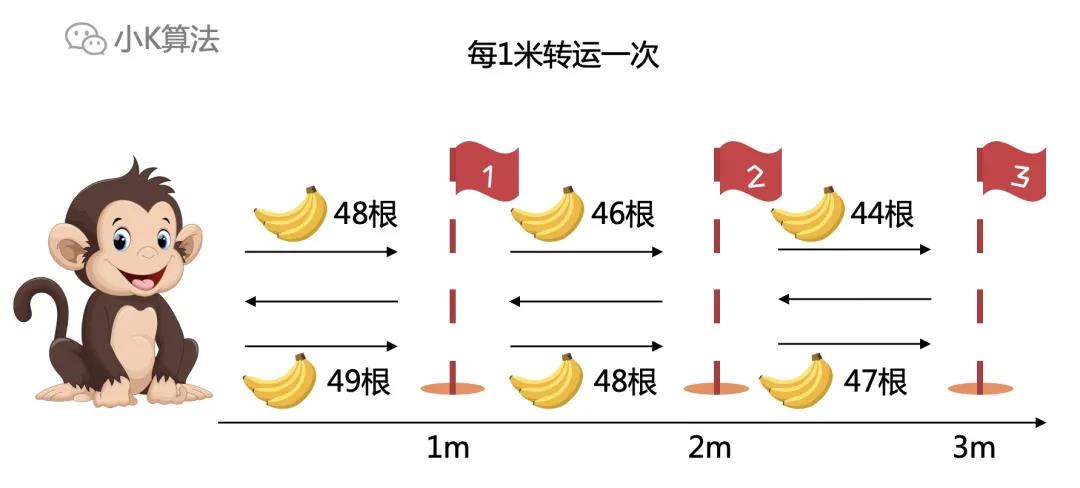

走到16米的地方还有一个特别的点。现在还有52根香蕉，距离家还有34米。此时只拿50根回家，不要多出的2根，也能搬回16根香蕉。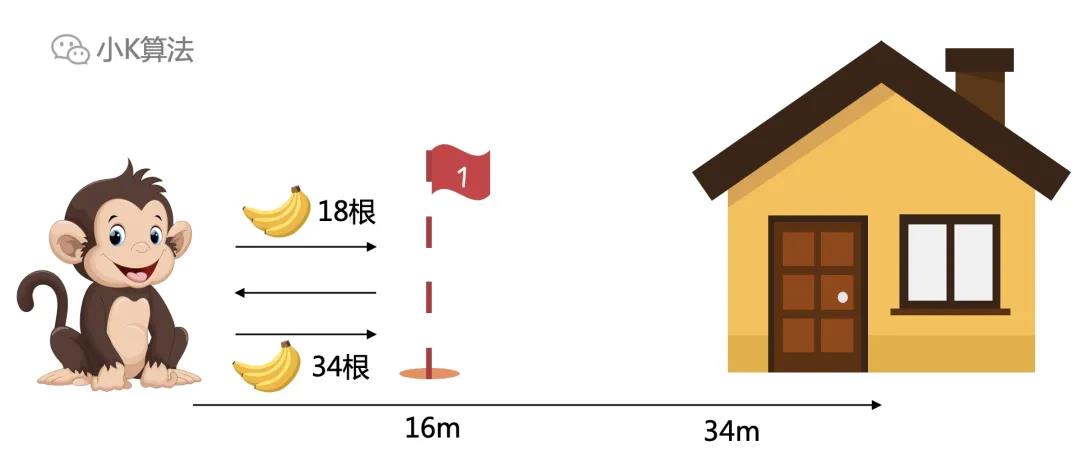

05 总结

这类问题最直观的第一感觉，就是越到后面阶段，运输效率越低，所以能想到中转。跟现实生活中的快递运输是一样的，快递也会有很多的中转站。中转站的设立是可以无限微分划区间，再用积分来计算，但这样就太复杂了，所以用分段的思想能解决大部分的问题。

文章来源：小K算法