题目

题解

• 法一：
  将二叉搜索树的中序遍历的结果存入数组中，取数组的第k个结果。

  function KthNode(pRoot, k)
  {
      if(!pRoot || k<1) return;
      return gotoArr(pRoot)[k-1];
  }
  let res = [];
  function gotoArr(root){
      // 中序遍历结果存入数组
      if(!root) return;
      gotoArr(root.left);
      res.push(root);
      gotoArr(root.right);
      return res;
  }

  存在问题：需要将所有结点遍历完，时间复杂度高

// 》》改进版《《
let res = [];
let key; // flag：确定是否取到结果
function KthNode(pRoot, k)
{
    if(!pRoot || k<1) return;
    key = k;
    return gotoArr(pRoot)[k-1];
}

function gotoArr(root){
    // 中序遍历结果存入数组
    if(res.length === key) return; //取到结果，停止
    if(root.left) gotoArr(root.left);
    res.push(root);
    if(root.right) gotoArr(root.right);
    return res;
}

• 法二：
  中序遍历二叉搜索树，搜索至第k个结点时，停止。

  function KthNode(root, k)
  {
      if(!root || k<1)return null;
      let res = null;
      // 为了追踪k值，将中序遍历函数定义在里面
      function traverse(root){
          if(!root) return null;
          if(root.left) res = traverse(root.left);
          if(!res){
              // 左子树未查找到结果
              if(k===1) res=root;
              k--;
          }
          if(root.right) res = traverse(root.right);
          return res;
      }
      return traverse(root);
  }

补充知识点：

二叉搜索树：

a. 定义:

二分搜索树（Binary Search Tree），也称为二叉查找树 、二叉搜索树 、有序二叉树或排序二叉树。满足以下几个条件：

• 若它的左子树不为空，左子树上所有节点的值都小于它的根节点。
• 若它的右子树不为空，右子树上所有的节点的值都大于它的根节点。
  它的左、右子树也都是二分搜索树。如下图所示：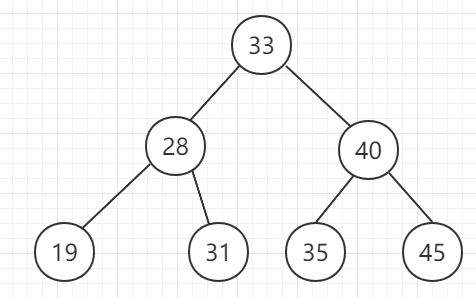
  

b. 二分搜索树有着高效的插入、删除、查询操作。

平均时间的时间复杂度为 O(log n)，最差情况为 O(n)。二分搜索树与堆不同，不一定是完全二叉树，底层不容易直接用数组表示故采用链表来实现二分搜索树。

c. 二分查找法过程
二分查找法的思想在 1946 年提出，查找问题是计算机中非常重要的基础问题，对于有序数列，才能使用二分查找法。如果我们要查找一元素，先看数组中间的值V和所需查找数据的大小关系，分三种情况：

• 1、等于所要查找的数据，直接找到
• 2、若小于 V，在小于 V 部分分组继续查询
• 2、若大于 V，在大于 V 部分分组继续查询

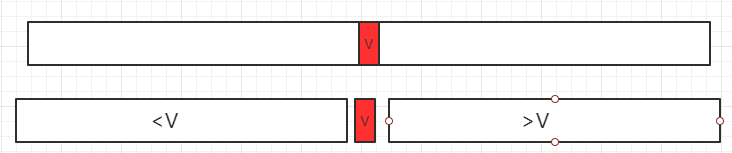
代码:

var search = function(nums, target) {
    let [start,end] = [0,nums.length-1];
    let middle,midItem;// 中间元素索引以及内容
    while(start<=end){
        middle = Math.floor((start+end)/2);
        midItem = nums[middle];
        if(midItem === target){
            return middle;
        }            
        else if(midItem > target){
            end = middle-1;
        }
        else{
            start = middle+1;
        }
    }
    return -1;

};