题目
给你一个整数 n ,请你返回所有 0 到 1 之间(不包括 0 和 1)满足分母小于等于 n 的 最简 分数 。分数可以以 任意 顺序返回。
解题思路
题目本意实际上是判断两个数是否为互质数,如果是则构成的分数返回。
判断两个数是否为互质数有两种方法:欧几里得算法和更相减损法。
- 欧几里得算法
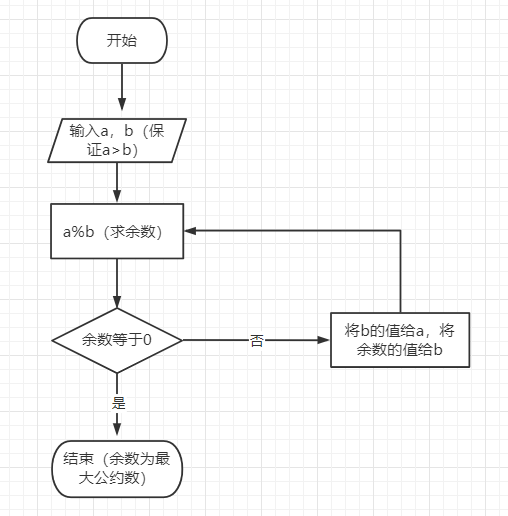
算法过程:大数放a中,小数放b中。大数除以小数,余数为零,则小数为最大公约数,不为零则将余数与b比较大的放a,小的放b,如此往复!
1 | //欧几里得算法(辗转相除法) |
- 更相减损法
算法过程:用两个数中的较大值减去较小值,直至两数相等,得到的相等的数就是两个数的最大公约数。
1 | //更相减损法 |
解题代码
欧几里得算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17var simplifiedFractions = function(n) {
//欧几里得算法(辗转相除法)
function gcd(a,b){
if(a<b) [a,b] = [b,a];
return b == 0 ? a : gcd(b,a%b);
}
let res =[];
for(let i=1;i<n;++i){
for(let j=i+1;j<=n;j++){
if(gcd(i,j)===1) res.push(i+'/'+j);
}
}
return res;
};更相减损法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20var simplifiedFractions = function(n) {
//更相减损法
function GXJS(a,b){
while(true){
if(a>b) a-=b;
else if(a<b) b-=a;
else return a;
}
}
let res =[];
for(let i=1;i<n;++i){
for(let j=i+1;j<=n;j++){
// if(gcd(i,j)===1) res.push(i+'/'+j);
if(GXJS(i,j)===1) res.push(i+'/'+j);
}
}
return res;
}
