题目链接

题目

给你一个仅由整数组成的有序数组，其中每个元素都会出现两次，唯有一个数只会出现一次。

请你找出并返回只出现一次的那个数。

你设计的解决方案必须满足 O(log n) 时间复杂度和 O(1) 空间复杂度。

解题思路

题目要求解决方案必须满足 O(log n) 时间复杂度，可以使用二分查找解题。

对于子序列而言，可以通过子序列长度来判断结果是否存在。

• 如果长度为 偶数 ，则结果 不存在
• 如果长度为 奇数 ，则结果 存在 【因为成双成对的元素中存在一个单身狗】

在二分查找过程中存在3种情况：

1. 中间元素就是结果，此时 nums[mid]!==nums[mid-1] && nums[mid]!==nums[mid+1]【最好的情况了】
2. 中间元素与前一个元素相同，此时 nums[mid]===nums[mid-1]
3. 中间元素与后一个元素相同，此时 nums[mid]===nums[mid+1]
   对于2,3两种情况，需要通过左右两个子序列的长度判断结果存在哪一侧。

当结束二分查找还没有返回结果，那么此时一定是left>right，那么结果就是nums[right]

解题代码

var singleNonDuplicate = function(nums) {
    //必须满足 O(log n) 时间复杂度 --> 二分查找
    //对于子序列而言：偶数->不存在，奇数->存在
    let [left,right]=[0,nums.length-1];
    while(left<right){
        let mid = left+(right-left>>1);
        if(nums[mid]===nums[mid-1]){
            //此时要判断两边的长度是奇数还是偶数
            if((right-mid)%2===0){
                right = mid-2;
            }else{
                left = mid+1;
            }

        }else if(nums[mid]===nums[mid+1]){
            if((mid-left)%2===0){
                left = mid+2;
            }else{
                right = mid-1;
            }
        }else{
            return nums[mid];
        }
    }
    return nums[right];

};

更多的思考

其实如果抛开题目要求的解决方案必须满足 O(log n) 时间复杂度，还可以采取位运算的方法。

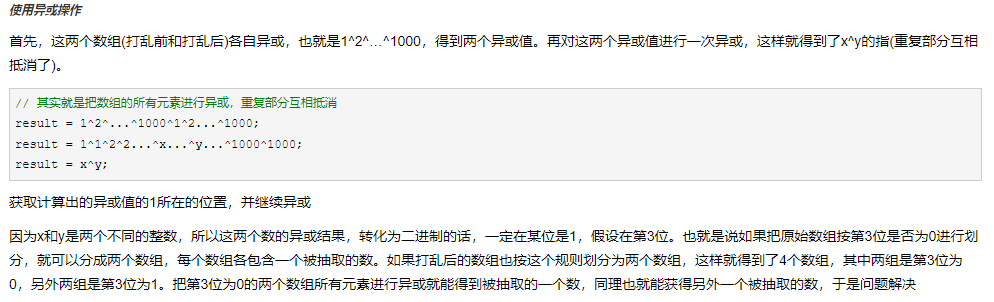
异或操作

异或是一种基于二进制的位运算，用符号XOR或者 ^ 表示，其运算法则是对运算符两侧数的每一个二进制位进行比较，同值取0，异值取1。

例如：1^4=3 —> (001) ^ (100) = (101)

异或操作的运算法则

1. a ^ b = b ^ a
2. a ^ b ^ c = (a ^ b) ^ c = a ^ (b ^ c)
3. d = a ^ b ^ c 可以推出 a = d ^ b ^c
4. a ^ b ^ a = b 【很重要的一个性质】

异或操作的典型题目

Q1: 对于一个有多个数值的数组，只有一个是唯一的，其他都是成对的，怎样快速找到这个唯一值。

其实就是这道题目的另一种说法，因此本题抛开时间复杂度的话，还可以使用异或操作的方法解决。

var singleNonDuplicate = function(nums) {
    let res = nums[0];
    for(let i=1;i<nums.length;++i){
        res^=nums[i];
    }
    return res;
};

Q2: 给你1-1000个连续自然数，然后从中随机去掉两个，再打乱顺序，要求只遍历一次，求出被去掉的两个数。

方法1：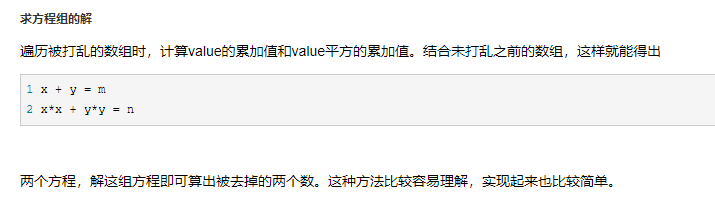

方法2：